FitzHugh#
FitzHugh() - the FitzHugh4 model without external stimulus.
The FitzHugh model is commonly used to test ODE software 10 6, the model itself describes the excitation state of a neuron membrane as an excitation spike passes. PyGOM also includes other functions which are commonly used to test numerical integrators such as:
vanDerPol() - the Van der Pol oscillator 12 and
Robertson() - the Robertson reaction 11.
The FitzHugh model equations are as follows:
\[\begin{split}\begin{aligned}
\frac{\mathrm{d} V}{\mathrm{d} t} &= c ( V - \frac{V^{3}}{3} + R) \\
\frac{\mathrm{d} R}{\mathrm{d} t} &= -\frac{1}{c}(V - a + bR).
\end{aligned}\end{split}\]
We solve for the deterministic time evolution of the system:
import numpy as np
from pygom import common_models
import matplotlib.pyplot as plt
ode = common_models.FitzHugh({'a':0.2, 'b':0.2, 'c':3.0})
t = np.linspace(0, 20, 101)
x0 = [1.0, -1.0]
ode.initial_values = (x0, t[0])
solution = ode.solve_determ(t[1::])
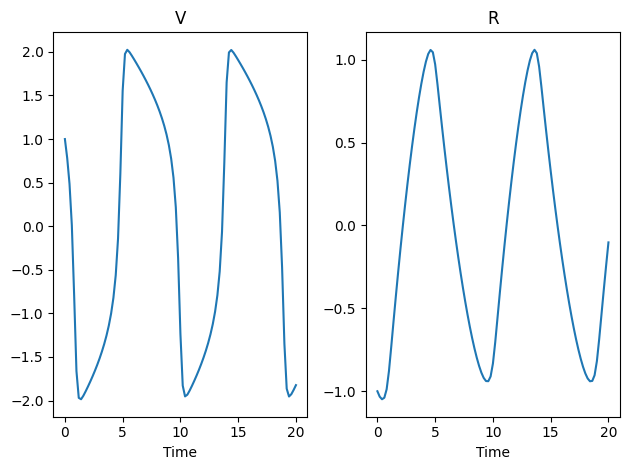
Plotting the function reveals frequent sharp transitions, which makes it an appropriate system to test ODE solving methods.
Show code cell source
ode.plot()