Time dependent parameters

Time dependent parameters#

PyGOM may also be used to model systems with time dependent parameters. Such situations commonly enter epidemic modelling if, for example, the infectivity varies with time due to seasonal effects or interventions. As an example, let’s consider an SIR model with periodic infectivity (\(\beta(t)\)) and add in immune waning too (so we can witness multiple seasons):

\[\begin{split}\begin{aligned} \frac{\mathrm{d} S}{\mathrm{d} t} &= -\frac{\beta(t) SI}{N} + w R + a S\\ \frac{\mathrm{d} I}{\mathrm{d} t} &= \frac{\beta(t) SI}{N}- \gamma I \\ \frac{\mathrm{d} R}{\mathrm{d} t} &= \gamma I - w R \\ \beta(t) &= \beta_0 \left(1-\delta \cos \left(\frac{2 \pi t}{P} \right) \right) \end{aligned}\end{split}\]

where \(\beta_0\) is some baseline infection rate, \(\delta\) is the magnitude of oscillations from the baseline (\(-1<\delta<1\) so that \(\beta>0\)), \(P\) is the oscillation period and \(w\) is the waning rate.

The variable, \(t\), has a special status in PyGOM, so that if it is found within a function it will be interpreted as referring to time. We must also provide the functional form of \(\beta\) which we do by including it as a derived parameter. In the following we put all of these requirements into code:

from pygom import SimulateOde, Transition, TransitionType, Event
import matplotlib.pyplot as plt
import numpy as np

# Define SIR model
stateList = ['S', 'I', 'R']                                    # now we have added tau to the states
paramList = ['gamma', 'N', 'beta0', 'delta', 'period', 'w', 'a']
derived_param = [('betaT', 'beta0*(1-delta*cos(2*3.14159*t/period))')]

# Infection
## Internal
transition_infection_int=Transition(origin='S', destination='I', transition_type='T')
event_infection_int=Event(transition_list=[transition_infection_int], rate='betaT*S*I/N')
## External importation
transition_infection_ext=Transition(origin='S', destination='I', transition_type='T')
event_infection_ext=Event(transition_list=[transition_infection_ext], rate='a*S')

# Recovery
transition_recovery=Transition(origin='I', destination='R', transition_type='T')
event_recovery=Event(transition_list=[transition_recovery], rate='gamma*I')

# Waning
transition_waning=Transition(origin='R', destination='S', transition_type='T')
event_waning=Event(transition_list=[transition_waning], rate='w*R')

# Set parameter values
gamma=0.25    # Recovery rate
n_pop=1e4     # Total population
beta0=0.3     # Baseline infectivity
period=365    # Period 1 year
delta=0.2     # beta varies between 0.8 and 1.2 times beta0
w=2/(365)     # timescale of immune waning of order 0.5 year
a=50/(365*n_pop)  # roughly 50 introductions per year

params=[('gamma', gamma),
        ('N', n_pop),
        ('beta0', beta0),
        ('delta', delta),
        ('period', period),
        ('w', w),
        ('a', a)]

# Initial conditions
i0=0
x0 = [n_pop-i0, i0, 0]

# Time range and increments
tmax=5*365                           # run for 10 years
dt=10                                 # time intervals for output
n_timestep=int(tmax/dt)               # number of iterations
t = np.linspace(0, tmax, n_timestep)  # times at which solution will be evaluated

# Set up pygom object
model = SimulateOde(stateList,
                    paramList,
                    event=[event_infection_int, event_infection_ext, event_recovery, event_waning],
                    derived_param=derived_param)

model.initial_values = (x0, t[0])  # (initial state conditions, initial timepoint)
model.parameters=params

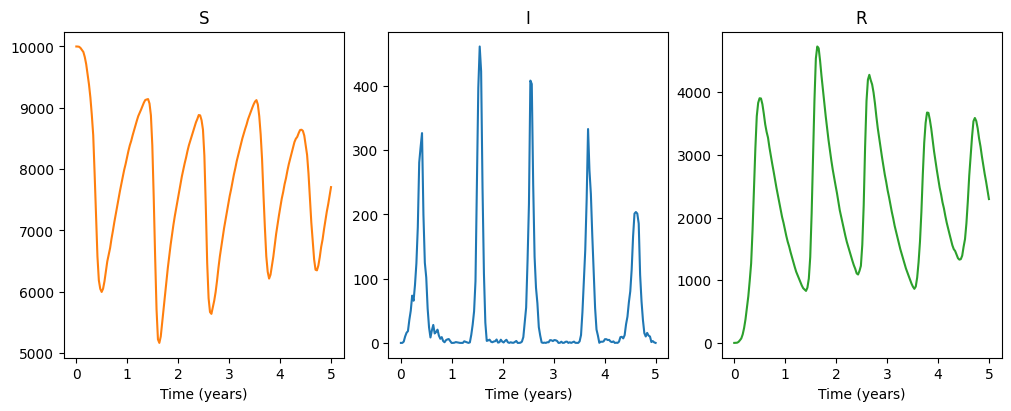
We may then solve this, for now let’s do so stochastically, and plot the result:

np.random.seed(1)
solution, simJump, simT = model.solve_stochast(t, 1, full_output=True)

../_images/69d7a655d0e0e735fe3ddf36724396b9dbf6d5cec3eeefb2a535a0b197b76e66.png