SIS, periodic#
This is an extension of the SIS model which incorporates a periodic infection rate, \(\beta(t)\). This could be used to mimic seasonal variation in infectivity due to yearly contact rate patterns or climate drivers, for example. We define \(\beta(t)\) as follows:
\[\begin{aligned}
\beta(t) &= \beta_0 \left(1+\delta \cos \left(\frac{2 \pi t}{P} \right) \right)
\end{aligned}\]
where \(\beta_0\) is the baseline infection rate, \(\delta\) is the magnitude of oscillations from the baseline (\(-1<\delta<1\) so that \(\beta>0\)) and \(P\) is the period of oscillations.
Also, note how we can use \(I+S=N\) to eliminate the equation for \(S\):
\[\begin{split}\begin{aligned}
\frac{\mathrm{d}I}{\mathrm{d}t} &= (\beta(t)N - \alpha) I - \beta(t)I^{2} \\
\end{aligned}\end{split}\]
In Heathcote’s classical model, \(\gamma=1\) and:
\[\begin{split}\begin{aligned}
\beta(t) &= 2 - 1.8 \cos(5t) \\
&= 2\left(1 - 0.9 \cos \left( \frac{2 \pi t}{ \frac{2 \pi}{5} } \right) \right)
\end{aligned}\end{split}\]
so that \(\beta_0=2\), \(\delta=0.9\) and \(P=\frac{2 \pi}{5}\).
from pygom import common_models
import matplotlib.pyplot as plt
import numpy as np
import math
# Set up PyGOM object
n_pop = 1e4
model = common_models.SIS_Periodic(
{
'gamma': 1,
'beta0': 2,
'delta': 0.9,
'period': (2*math.pi/5), 'N':n_pop
}
)
# Time range and increments
tmax = 10 # maximum time over which to run solver
dt = 0.01 # timestep
t = np.arange(0, tmax, dt)
# Initial conditions
i0 = 0.1 * n_pop
s0 = n_pop - i0
x0 = [s0, i0]
model.initial_values = (x0, t[0])
solution = model.solve_deterministic(t)
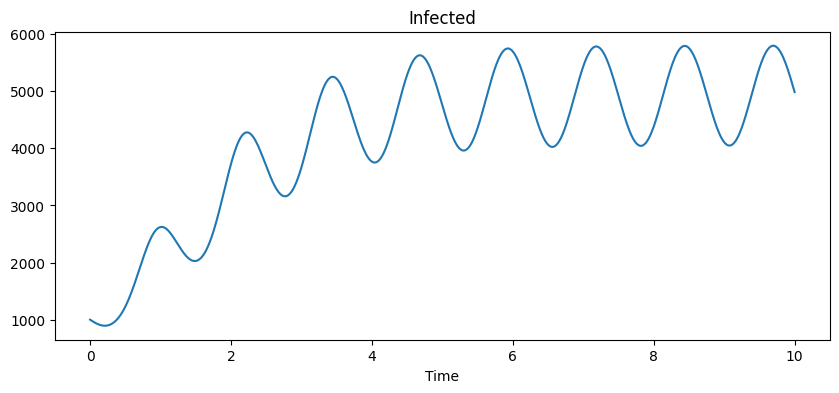
We plot the infected trajectory which shows periodic evolution.
Show code cell source
fig, axes = plt.subplots(figsize=(10, 4))
i = 1
axes.set_xlabel("Time")
axes.set_title(model.state_list[i])
axes.plot(t, solution[0].result.y[:, i])
plt.show()
