SEIR, multiple

SEIR_Multiple()

Multiple SEIR coupled together, without any birth death process.

\[\begin{split}\begin{aligned} \frac{\mathrm{d} S_{i}}{\mathrm{d} t} &= dN_{i} - dS_{i} - \lambda_{i}S_{i} \\ \frac{\mathrm{d} E_{i}}{\mathrm{d} t} &= \lambda_{i}S_{i} - (d+\epsilon)E_{i} \\ \frac{\mathrm{d} I_{i}}{\mathrm{d} t} &= \epsilon E_{i} - (d+\gamma) I_{i} \\ \frac{\mathrm{d} R_{i}}{\mathrm{d}t} &= \gamma I_{i} - dR_{i} \end{aligned}\end{split}\]

where

\[\lambda_{i} = \sum_{j=1}^{n} \beta_{i,j} I_{j} (1\{i\neq j\} p)\]

with \(n\) being the number of patch and \(p\) the coupled factor.

from pygom import common_models

import numpy

paramEval = {'beta_00':0.0010107, 'beta_01':0.0010107, 'beta_10':0.0010107, 'beta_11':0.0010107,
             'd':0.02, 'epsilon':45.6, 'gamma':73.0, 'N_0':10**6,'N_1':10**6,'p':0.01}

x0 = [36139.3224081278, 422.560577637822, 263.883351688369, 963174.233662546]

ode = common_models.SEIR_Multiple(param=paramEval)

t = numpy.linspace(0, 40, 100)

x01 = []

for s in x0:  
    x01 += 2*[s]

ode.initial_values = (numpy.array(x01, float),t[0])

solution, output = ode.integrate(t[1::], full_output=True)

ode.plot()

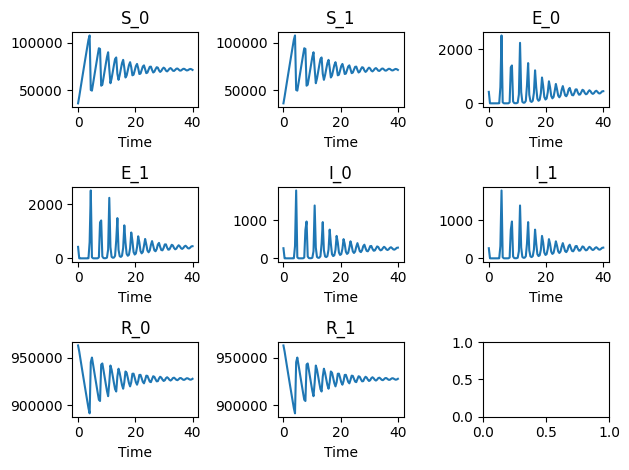
The initial conditions are those derived by using the stability condition as stated in Lloyd and May⁸ while the notations is taken from Brauer¹.